Programming Model
The first order of business is Maru's programming model. As a verifiable streaming computation platform, Maru is quite powerful and can do a great many things. However, it operates under a different computational model than you're probably used to - it's quite different from the EVM, an API, or a database. To help you build a conceptual framework for Maru's programming model, let's sketch out some key terms, their roles, and how they interact:
| Component | Role |
|---|---|
| Record | A single, small-ish element of arbitrary data. |
| Collection | An unordered set of records that keeps track of how many copies of each record are in the set. Analogous to a "multiset" or a "bag". You can think of it like a set of (record, count) pairs. |
| Delta | An incremental update to a collection, consisting of a record and difference in the number of instances of that record. e.g. (data, 1) means "insert 1 instance of data to the collection", while (data, -1) means "delete 1 instance of data from the collection". |
| Stream | An ordered stream of deltas, where each delta has a logical timestamp T. Streams are periodically accumulated into collections (i.e. "adding" together all of the deltas). |
| Operator | A single compute element that takes any number of input streams and produces any number of output streams. Specifically, it's a function that takes in one or more input deltas and outputs one or more corresponding deltas to be applied to the output. Operators are highly composable. |
| Source | A stream that comes from an external data source - it is not the output of any operator. |
| Sink | A stream that is not the input of any operator - instead, it's pushed to a user / external consumer. |
| Dataflow | A structured network of operators - the outputs of one can serve as inputs for another. The result is something resembling a directed-acyclic graph (DAG) of operators. |
Collections of Records vs Streams of deltas
Maru state is made up of Collections of Records. Since collections can get quite large and are updated frequently, instead of storing the collections and performing updates directly, instead we process Streams of deltas - tiny incremental changes to state. Then, we periodically "combine" or "fold" all of the deltas together, reconstruct a "snapshot" of the underlying collection, and store it somewhere cheap.
This is not only more efficient to process but also more efficient to prove, since most streaming computations can be broken down into many tiny pieces. Not only are deltas cheap to prove, but they can be proven in parallel.
Operators
If you're a developer, you've propably seen JavaScript code that does something like this:
let res = collection
.map(x => /* return a transformation of x */)
.filter(x => /* return a boolean */)
.reduce((acc, x) => /* return a new accumulator given x*/)
// etc
Conceptually, operators are a generalization of the map, filter, reduce methods in JavaScript - an iterator over a collection is fed into the operator, and it processes each element, spitting the result into a new output iterator.
Unlike JavaScript, you can write your own operators - you're not limited to map, filter, reduce, or some other operator that's already implemented in the langauge. More importantly, also unlike JavaScript, the "streams" aren't Collections of Records, they're Streams of deltas. That means the following:
Your operator isn't answering the question "given an input collection, what's the output collection?", it's answering the question "given a change to the input collection, what corresponding changes do we need to make to the output collection?"
This might be the trickiest part of Maru's programming model to grok, and it comes more naturally the more you think about it. That said, here are some helpful thought-bites to help you wrap your head around it:
mapis exactly the same with deltas as it is with collections.filteris too.- To implement a
sumincrementally, multiply therecordby itscount- if the count is negative, we'll subtract the record's value from the sum, which is exactly what we want to do. - Most Stateful (Min, Sort, Join, etc) operators can be implemented in a way that doesn't require reconstructing the underlying collection - just having access to previous deltas is sufficient.
- To read more about it, see the background knowledge section.
Dataflow
One of Maru's greatest strengths is the fact that operators are composable - the output of one can feed into the input for another. Furthermore, Operators needn't be unary - they can have any number of inputs and/or outputs. And since every operator's output is proven, anyone can trustlessly compose one operator off of another, encouraging work-sharing.
If we were to visualize the structure of the operators feeding one into another, we'd end up with something looking like this:
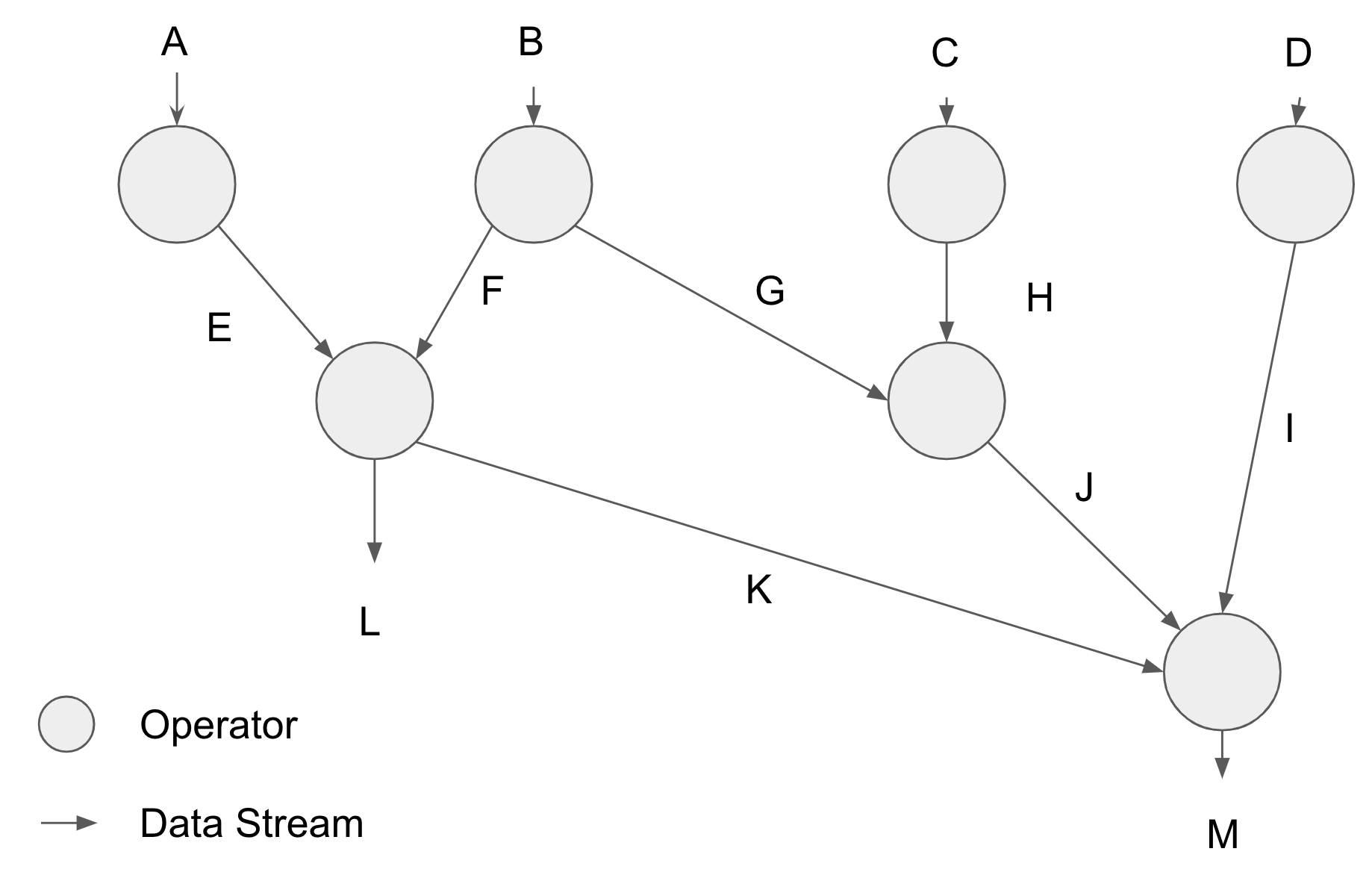
The real power of composability here isn't that developers don't need to implement their entire data pipeline from scratch, it's that, for each delta, each operator only needs to be executed and proven once, no matter how many downstream operators use the output. In this example, streams L, K, M, J, G, and F all use work of the operator at B, and thus the cost of it can be spread evenly across them all.
But that's not even the best part - stream composition also incentivizes applications to co-optimize their applications, extracting out common sub-operations and removing all redundant work. This incentive brings together teams working on separate products to contribute to Maru. In turn, Maru has more resources it can put into processing more data, leading to more co-optimization, leading to more data. It's a virtuous cycle that encourages a strong community to develop around making sure everyone's computation is fast, reliable, and cheap. You can read more about how this works in how-maru-works.