Architecture
In this chapter, we will list the high-level "modules" of Maru and briefly explain their purpose and how they fit together. Subsequent chapters will dive deeper into their respective components.
| Module | Role |
|---|---|
| Runtime | The VM for processing individual deltas and the STARK-prover for that VM. Feeds into Proof Pipeline under a developer-chosen Accumulation Strategy. |
| Proof Pipeline | An embarrassingly-parallel pipeline for recursively accumulating many thousands of proofs per second. |
| Arrangements | Manner in which a stream of deltas should be sorted / indexed. |
| Operator | An abstraction representing a single "compute element" in the dataflow - consists of runtime bytecode and a recursion strategy |
| Dataflow | Distributed system that moves deltas between operators and executes the proof pipeline. |
| Relayer Network | Network of nodes that subscribe to output stream(s) of the dataflow, compress the proofs, and submit them to the blockchain |
| Verifier Smart Contract | A smart contract that verifies the final proofs generated by the relayer network. |
At a high level, the architecture looks something like this:
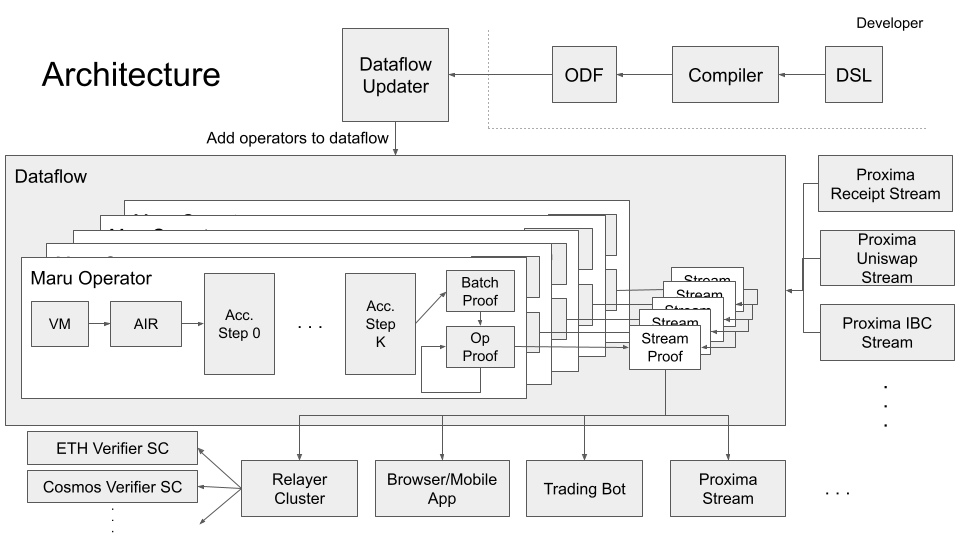
Dataflow
The "dataflow" is the underlying implementation of Maru operators and their composition. It can be thought of as a "DAG of operators" that is responsible for allocating work to operators and moving deltas from their origin to the operators that need them.
The centralized version of Maru builds atop differential Dataflow, itself a wrapper around Timely Dataflow. Maru simply extends the operator definitions in differential Dataflow with our prover pipeline and executes them through our runtime. See the dataflow chapter for details on how exactly we do this.
Operators
Operators are units of stream-handling logic specified by a developer. A developer implements their operator logic using a domain-specific-language (DSL). The compiler for this DSL outputs what is called an "operator definition", which includes the bytecode(s) for the operator(s) logic and a descriptor file that explains how to connect them together and "graft" them onto the global dataflow. You can read more about the DSL here.
Runtime
The runtime module consists of Aincrad, Maru's STARK-AIR that proves computational integrity (i.e. correctness) of an execution trace from the Aincrad Runner, our VM. The VM runs bytecode supplied to the dataflow via an Operator Definition File (ODF), which is discussed in adding operators to the dataflow.
Aincrad requires that all deltas needed in the computation be given to it up-front. This means that the dataflow is responsible for providing any historical deltas that need to be considered in order to produce the output delta(s), and therefore they must be defined up-front. Oftentimes this requires using a recursion strategy to arrange historical deltas in a way where this is feasible.
If you've ever written programs on Solana's runtime (Sealevel), this may seem quite familiar. Like Sealevel, Aincrad requires all accounts (state) to be provided as an explicit input at the beginning of execution. Unlike Sealevel, however, Aincrad take deltas as input instead of states.
Read more about the runtime at runtime.md
Proof Pipeline
The proof pipeline is the how Maru horizontally-scales. In the past two years, recursive SNARK performance has improved drastically. In particular, Plonky2 recursion takes ~180ms on my Macbook from 2019 for a reasonably-sized circuit, which makes it feasible to have 10, 20, even 50 layers of recursion, allowing Maru's throughput to scale linearly with the number of CPUs we can throw at it. And once Maru is decentralized, the amount CPUs going into Maru will be massive.
How does efficient proof recursion enable parallel proof generation? It allows us to execute a sequential computation but prove it in parallel. This is one of the core ideas behind Mina, and in Maru we utilize plonky2 to take this idea to its extreme.
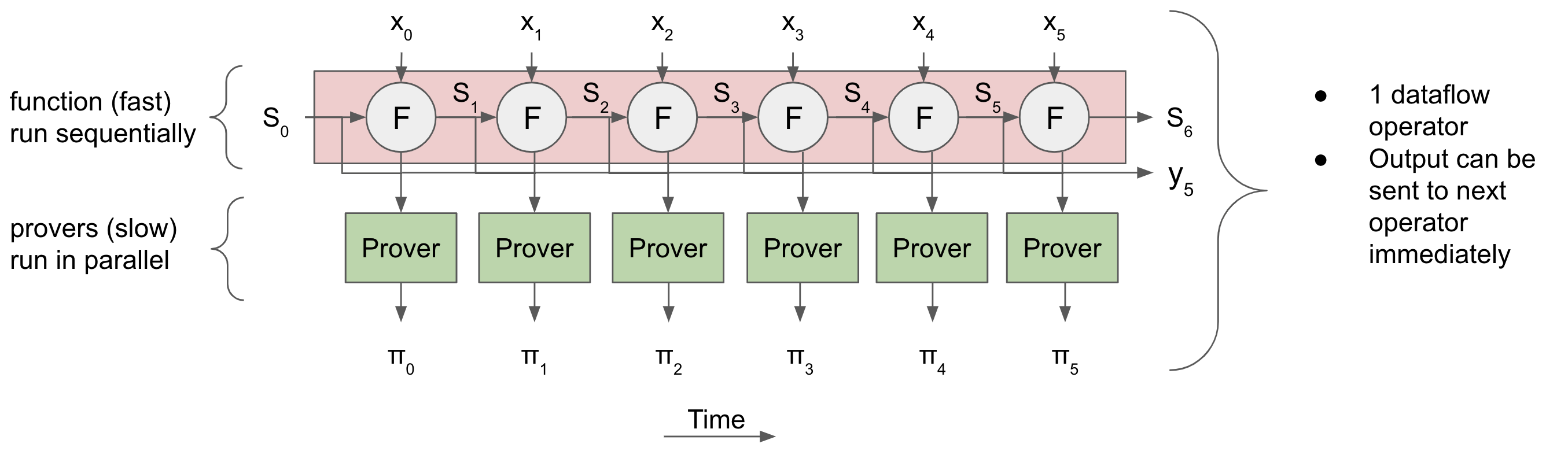
Then, we can use recursion to "merge" or "accumulate" all of the proofs together in a tree-like fashion. In this "accumulation tree", each layer only depends on the layer "below" it, so we can pipeline several batches of proof accumulation - At the same time, the first batch can be accumulated in the first layer of the tree, the second batch of STARK proofs can be generated, and the third batch of deltas can be processed.
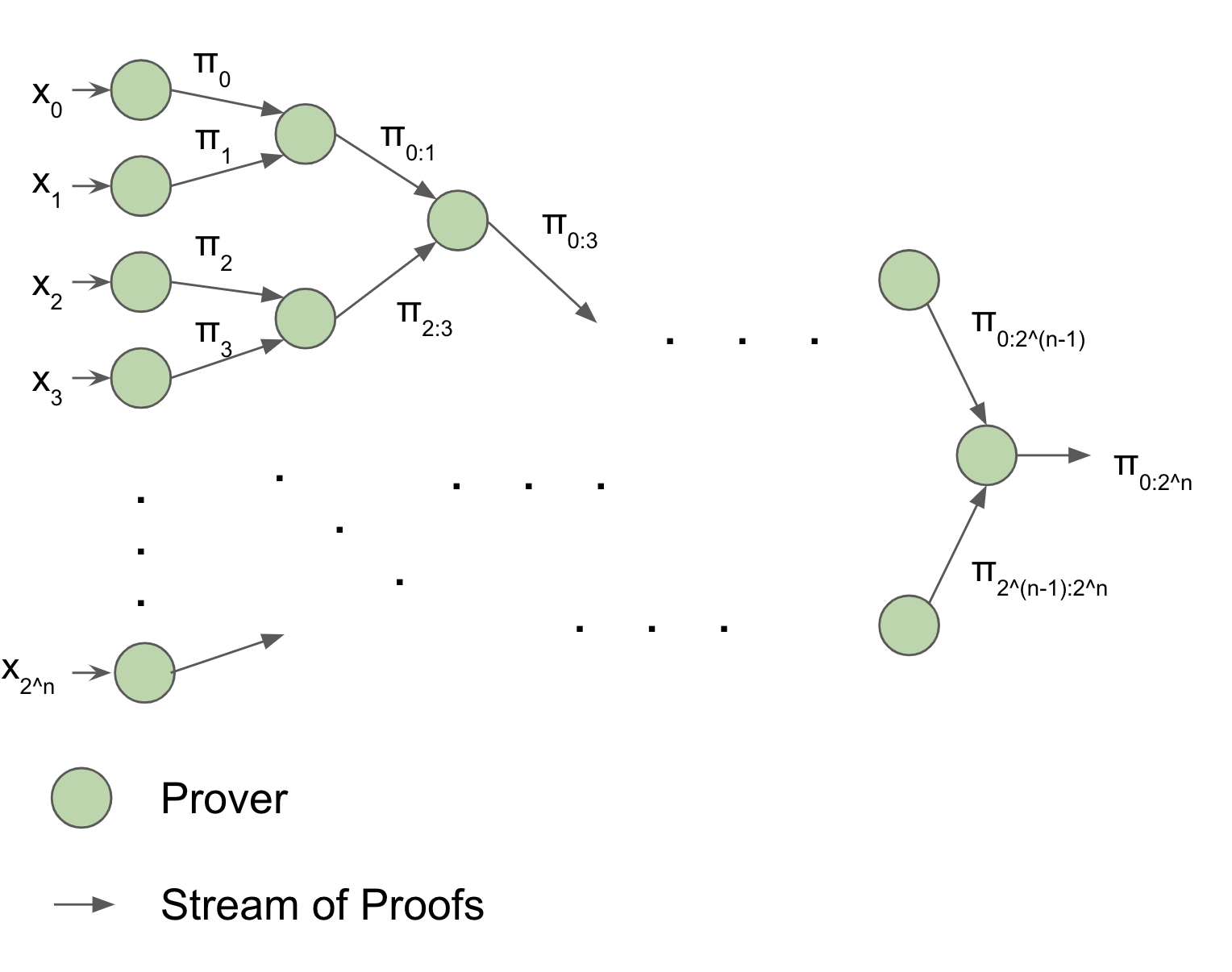
Everything is at full-utilization. And if we want to accumulate bigger batches, we can just add a layer to the tree. Then, as long as we have enough CPUs, throughput will double while latency will only increase by a fraction of a second. And at the end, the verifier only has to verify a single proof.
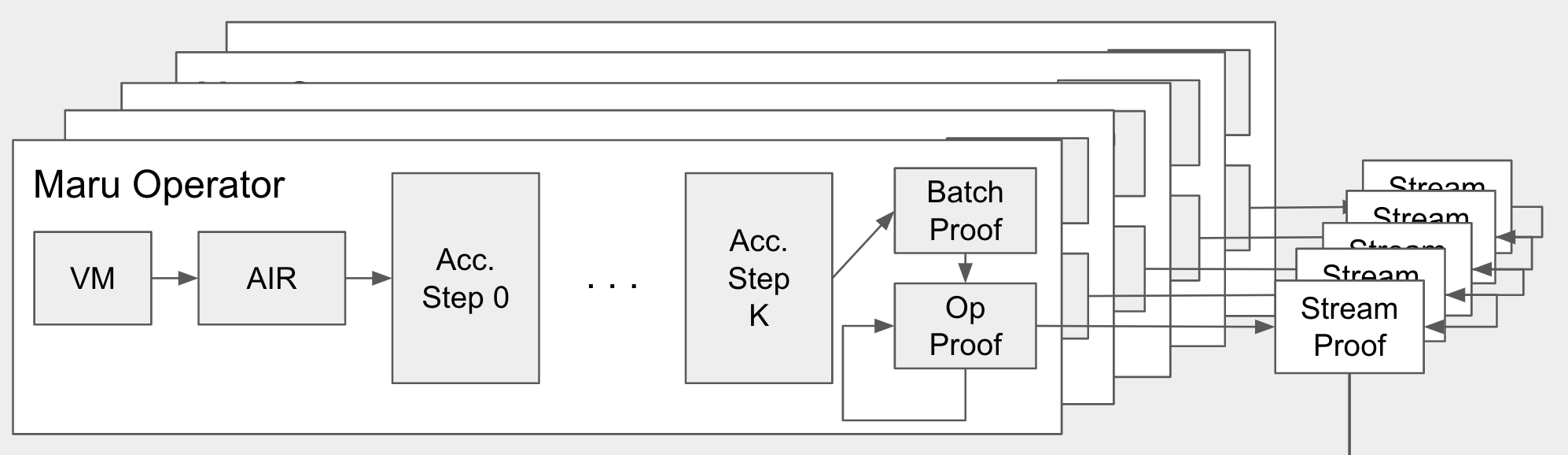
How does this fit into everything else? This proof accumulation tree corresponds to a single batch of deltas fed into a single operator. We can add more layers to prove a sequence of batches in parallel, and we can add even more layers to prove a sequence of batches for a sequence of operators in parallel, so the pipeline ends up looking something what's shown in the architecture diagram above (duplicated here to save your working memory):
Arrangements
Arrangements are indexed versions of a stream. These are needed because many efficient algorithms require random access to a stream's historical deltas. For example, min and max requires access to historical deltas, and in particular it needs to keep track of the current minimum or maximum of the records. This effectively amounts to a sharded "key-value store interface" for a collection. Differential Dataflow implements them as basic tries.
In Maru, however, it's not enough to simply index the streams, since, now that we're doing "random access" from a collection, we need membership proofs. Unfortunately, multiset hashes don't give us membership proofs, so we maintain arrangements as Merkle tries. We then use a special "arrangement STARK" to prove correctness of the updates to the arrangement against the stream's running multiset hash. This merkle root is elided away during proof accumulation, so the verifier still only needs the block hash to verify the proof. You can read more about how exactly we do this here.